Nesta aula apresentamos fatos sobre funções injetoras, sobrejetoras e bijetoras, introduzimos a noção de relação e classe de equivalência, bem como a noção de conjunto quociente.
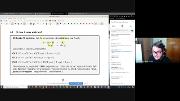
Nesta aula apresentamos diversos exemplos de métricas, dentre os quais a métrica associada à norma de um espaço vetorial normado e a métrica induzida em um subconjunto de um espaço métrico. Definimos a noção fundamental de bola aberta e apresentamos alguns exemplos.
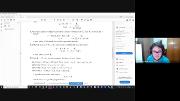
Nesta aula continuamos o estudo do conceito de bola aberta e introduzimos, em seguida, as noções de bola fechada e esfera. Apresentamos o conceito de pseudo-métrica e o conceito de seminormas, encerrando com a definição de espaço métrico limitado.
Nesta aula apresentamos a noção de normas equivalentes, bem como sua caracterização. Damos a definição de distância entre pontos e conjuntos, bem como a de distância entre subconjuntos quaisquer de um espaço métrico. Apresentamos a definição do diâmetro de um conjunto e definimos, de modo natural, três métricas no produto cartesiano de espaços métricos. Finalmente, apresentamos a noção de imersão isométrica e de isometria.
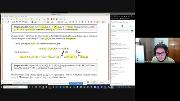
Nesta aula apresentamos a noção de isometria local e apresentamos um exemplo. Apresentamos a definição de ponto interior, de vizinhança de um ponto e de interior de um conjunto, o que nos permite dar a definição de conjunto aberto. Exibimos propriedades que caracterizam os abertos de um espaço métrico como topologia, e definimos os abertos relativos em um subespaço métrico.
Nesta aula abordamos o conceito de vizinhança de um subconjunto, de ponto isolado e espaço discreto. Em contraposição, vemos também o conceito de conjunto derivado e suas propriedades. Apresentamos a definição do fecho de um conjunto e, munidos desta, apresentamos a de conjunto fechado. Finalmente, caracterizamos o fecho de um conjunto como o menor conjunto fechado que o contém e caracterizamos um conjunto como fechado se, e somente se, for complementar de um conjunto aberto.
 Carregando
Carregando
 Carregando
Carregando