244
resultados encontrados

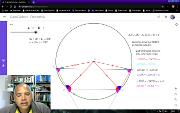
Demonstração da ida e da volta da proposição: Um quadrilátero é inscritível se, e somente se, os ângulos formados entre um lado e uma diagonal e o lado oposto e a outra diagonal forem iguais. Saber que quatro pontos no plano pertencem a uma circunferência (formam um quadrilátero inscritível) é de grande ajuda na resolução de problemas. Já tínhamos provado que "Um quadrilátero é inscritível se, e somente se, a soma dos ângulos opostos é 180 graus". Este vídeo está incluído na playlist Geometria com Geogebra. Mais em https://www.youtube.com/watch?v=j_85My--ZKQ&list=PL8v7luSb9qi6tg7XIcqfG_hT-qU-r4qS_&index=37.
Um trapézio isósceles é um quadrilátero com dois lados paralelos e os outros dois lados iguais (de igual medida). Se mostra que quatro pontos (A, B, C e D) que pertencem a uma circunferência, tais que AD=BC, determinam um trapézio isósceles. Este vídeo está incluído na playlist Geometria com Geogebra. Mais em https://www.youtube.com/watch?v=H9gpKCVIFOM&list=PL8v7luSb9qi6tg7XIcqfG_hT-qU-r4qS_&index=38.
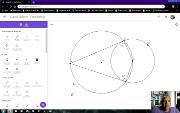
Se aprende como construir as retas tangentes a uma circunferência passando por um ponto externo a esta dado. Este vídeo faz parte da curso Geometria com Geogebra. Mais em https://www.youtube.com/watch?v=21g2h_WUaTU&list=PL8v7luSb9qi6tg7XIcqfG_hT-qU-r4qS_&index=3.
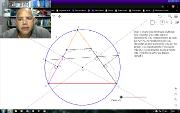
Segunda resolução (primeira no V36) do problema 1 da Olimpíada Internacional de Matemática (IMO, International Mathematical Olympiad) de 2018. Alguns dos conteúdos usados desta vez são: ângulos correspondentes entre paralelas como critério de paralelismo; quadriláteros inscritíveis; paralelogramos; triângulos isósceles e mediatriz. Este vídeo está incluído na playlist Geometria com Geogebra. Mais em https://www.youtube.com/watch?v=YZEU3dMH0Zc&list=PL8v7luSb9qi6tg7XIcqfG_hT-qU-r4qS_&index=39.
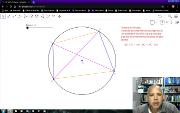
A ida do teorema de Ptolomeu diz que no quadrilátero inscritível (quatro pontos sobre uma mesma circunferência) ABCD o produto das diagonais é igual a soma dos produtos dos lados opostos. Isto é, sendo AC e BD suas diagonais, vale que: ABxCD + BCxAD = ACxBD. A volta do teorema também é verdadeira. Este vídeo está incluído na playlist Geometria com Geogebra. Mais em https://www.youtube.com/watch?v=cmjKvHsIv_w&list=PL8v7luSb9qi6tg7XIcqfG_hT-qU-r4qS_&index=40.

Se mostra que o Teorema de Pitágoras é obtido quando o quadrilátero usado no Teorema de Ptolomeu é um retângulo. Todo retângulo é inscritível pois a soma dos seus ângulos opostos é 90+90=180 graus. Se estuda um segundo problema com duas circunferências circunscritas a diferentes triângulo e um ponto em comum a todas as figuras. Este vídeo está incluído na playlist Geometria com Geogebra. Mais em https://www.youtube.com/watch?v=ZBJian3zE1Q&list=PL8v7luSb9qi6tg7XIcqfG_hT-qU-r4qS_&index=41.
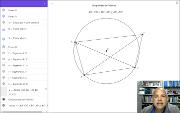
Se prova a Desigualdade de Ptolomeu, uma generalização do Teorema de Ptolomeu, onde o quadrilátero ABCD, de diagonais AC e BD, não precisa ser inscritível e vale que ACxBD é menor ou igual a ABxCD+BCxAD. No caso em que os pontos A, B, C e D são concíclicos (pertencem a uma mesma circunferência) vale a igualdade. Este vídeo está incluído na playlist Geometria com Geogebra. Mais em https://www.youtube.com/watch?v=x7nXqie9TdI&list=PL8v7luSb9qi6tg7XIcqfG_hT-qU-r4qS_&index=42.
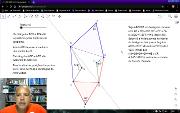
Problema 11 da "Short List" (SL) da Olimpíada Internacional de Matemática (IMO, International Mathematical Olympiad) de 1995. Alguns dos conteúdos usados na solução são: Teorema de Ptolomeu; Desigualdade de Ptolomeu; Hexágono; Reflexão; Desigualdade Triangular; Triângulos equiláteros, isósceles e mediatriz. Este vídeo está incluído na playlist Geometria com Geogebra. Mais em https://www.youtube.com/watch?v=qgWUPol3-YI&list=PL8v7luSb9qi6tg7XIcqfG_hT-qU-r4qS_&index=43.
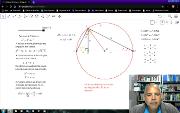
Se descreve a notação usada no triângulo retângulo para escrever as relações métricas. Se mostram os triângulos semelhantes e as equações de proporcionalidade dos lados. É feito um resumo com palavras e com fórmulas das expressões importantes de lembrar na hora de resolver problemas de olimpíadas e vestibulares. Se esboça a circunferência circunscrita e se recorda que a mediana correspondente ao ângulo reto é metade da hipotenusa. Este vídeo está incluído na playlist Geometria com Geogebra. Mais em https://www.youtube.com/watch?v=kI3_5_BXoMI&list=PL8v7luSb9qi6tg7XIcqfG_hT-qU-r4qS_&index=44.
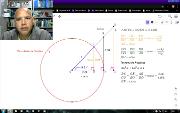
Se mostra que uma conjunto infinito de triângulos retângulos semelhantes podem ser representados por um de hipotenusa unitária. Se define Seno, Cosseno e Tangente de um ângulo. Se demonstra a identidade trigonométrica fundamental, consequência do Teorema de Pitágoras. Se introduz a ideia das funções trigonométricas no primeiro quadrante da circunferência de raio 1. Este vídeo está incluído na playlist Geometria com Geogebra. Mais em https://www.youtube.com/watch?v=O_MVXWQ9p1g&list=PL8v7luSb9qi6tg7XIcqfG_hT-qU-r4qS_&index=45.
244
resultados encontrados










