244
resultados encontrados
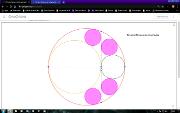
Arbelos é uma região plana delimitada por uma semicircunferência de raios r1+r2 e duas semi circunferências de diâmetros r1 e r2. Círculos gêmeos de Arquimedes são dois círculos congruentes, de raio R, inscritos em um arbelos. Sua construção é descrita no Livro dos Lemas, atribuído a Arquimedes. R é calculado como a metade da média harmônica de r1 e r2. Este vídeo está incluído na playlist Geometria com Geogebra. Mais em https://www.youtube.com/watch?v=C7ezR0FeFfM&list=PL8v7luSb9qi6tg7XIcqfG_hT-qU-r4qS_&index=59.

Solução do problema 15 da "Short List" da Olimpíada Internacional de Matemática (IMO, International Mathematical Olympiad) de 1994. Se explora o conceito de "Eixo Radical" e "Centro Radical" e aproveitam os passos de construção discutidos em duas aulas anteriores. Este vídeo está incluído na playlist Geometria com Geogebra. Mais em https://www.youtube.com/watch?v=aozdm2dJegM&list=PL8v7luSb9qi6tg7XIcqfG_hT-qU-r4qS_&index=58.
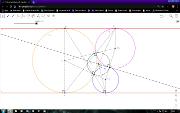
Segunda solução para o desafio da construção de três circunferências tangentes externas dois a dois e tangentes no interior de duas retas paralelas. Neste caso não é necessário calcular a raio da segunda circunferência pelo Teorema de Pitágoras. Se explora o conceito de "Eixo Radical" e "Centro Radical". Preparação para discutir o problema 15 da "Short List" da Olimpíada Internacional de Matemática (IMO, International Mathematical Olympiad) de 1994. Este vídeo está incluído na playlist Geometria com Geogebra. Mais em https://www.youtube.com/watch?v=px10G8OUa9g&list=PL8v7luSb9qi6tg7XIcqfG_hT-qU-r4qS_&index=57.
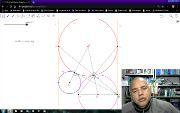
Uma solução para o desafio da construção de três circunferências tangentes externas dois a dois e tangentes no interior de duas retas paralelas. Este vídeo está incluído na playlist Geometria com Geogebra. Mais em https://www.youtube.com/watch?v=Xz-LmBcHTsU&list=PL8v7luSb9qi6tg7XIcqfG_hT-qU-r4qS_&index=56.
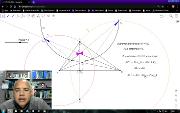
Se resolve o desafio: Seja ABC um triângulo tal que ∠BCA = 90◦, e seja C0 o pé da altura relativa a C. Seja X um ponto no interior do segmento CD. Seja K o ponto do segmento AX tal que BK = BC. Analogamente, seja L o ponto do segmento BX tal que AL = AC. Seja M o ponto de interseção de AL com BK. Provar que MK = ML. Problema 5 da Olimpíada Internacional de Matemática (IMO, International Mathematical Olympiad) de 2012. Este vídeo está incluído na playlist Geometria com Geogebra. Mais em https://www.youtube.com/watch?v=ZUdmo7Aw-Y8&list=PL8v7luSb9qi6tg7XIcqfG_hT-qU-r4qS_&index=55.

Se soluciona o desafio a seguir: Em um triângulo ABC, a bissetriz do ângulo A e a mediana relativa a BC intersectam este lado em pontos distintos O e M, respectivamente. O círculo circunscrito ao triângulo AOM intersecta os lados AB e AC em E e F, respectivamente. Provar que BE = CF. Este vídeo está incluído na playlist Geometria com Geogebra. Mais em https://www.youtube.com/watch?v=CB4bRUc-Tzc&list=PL8v7luSb9qi6tg7XIcqfG_hT-qU-r4qS_&index=54.
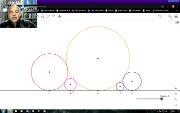
Se apresenta o desafio de construir com régua e compasso, ou usando um software de geometria dinâmica, cinco circunferências tangentes dois a dois e a uma linha. Basta lembrar do significado de reta tangente, usar o Teorema de Pitágoras e resolver um sistema de equações. Este vídeo está incluído na playlist Geometria com Geogebra. Mais em https://www.youtube.com/watch?v=PdlYN1oR4Vk&list=PL8v7luSb9qi6tg7XIcqfG_hT-qU-r4qS_&index=51.
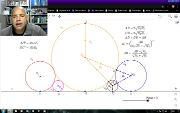
Se soluciona o desafio de construir com régua e compasso, ou usando um software de geometria dinâmica, cinco circunferências tangentes dois a dois e a uma linha. Basta lembrar do significado de reta tangente, usar o Teorema de Pitágoras e resolver um sistema de equações. Este vídeo está incluído na playlist Geometria com Geogebra. Mais em https://www.youtube.com/watch?v=tV20hdfLGAM&list=PL8v7luSb9qi6tg7XIcqfG_hT-qU-r4qS_&index=52.
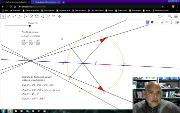
Se estuda um invariante geométrico chamado potência de um ponto P relativo a uma circunferência c, de centro O de raio r, ou simplesmente potência de P. Partindo de P são traçadas duas retas que cortam a c nos pontos A, B e C, D, respetivamente. Se mostra que Pot_c(P)=PAxPB=PCxPD. Isto é, a potência de P não depende da corda usada. Usando o diâmetro como corda pode-se escrever Pot_c(P)=d^2-r^2, onde d é a distância de P a O. A potência é positiva quando P é exterior a c, zero quando P é um ponto de c e negativa quando é interior a c. Quando se usa o segmento PF, tangente a c em F, temos Pot_c(P)=PF^2. Este vídeo está incluído na playlist Geometria com Geogebra. Mais em https://www.youtube.com/watch?v=Rj_CsTBKCug&list=PL8v7luSb9qi6tg7XIcqfG_hT-qU-r4qS_&index=53.
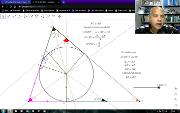
Solução do desafio a seguir: No triângulo ABC, o incírculo, com centro I, toca o lado BC no ponto D. A linha DI encontra AC em X. A linha tangente de X com o incírculo (diferente de AC) intercepta AB em Y. Se YI e BC se intersectam no ponto Z, provar que AB = BZ. Problema 1 (Nível Avançado) da 4 Olimpíada Iraniana de Geometria (IGO, Iranian Geometry Olympiad) de 2017. Este vídeo está incluído na playlist Geometria com Geogebra. Mais em https://www.youtube.com/watch?v=4Tar1BnyaBc&list=PL8v7luSb9qi6tg7XIcqfG_hT-qU-r4qS_&index=50.
244
resultados encontrados










