3685
resultados encontrados

Nesta aula vamos estudar o fenômeno de difração e relacioná-lo à teoria matemática de transformada de Fourier.

As rotações finitas podem ser descritas por uma quantidade que tem módulo direção e sentido, mas que não é um vetor, porque a soma de duas rotações finitas não é comutativa. No entanto, as rotações infinitesimais são vetores, de modo que é possível definir vetores velocidade e aceleração angular.

Resolvemos os exercícios 2, 5 e 6 da lista 5, que procuram mostrar que tudo que aprendemos acerca de derivadas e integrais nos movimentos de translação aplicam-se ao movimento de rotação.

Discutimos que o movimento de um corpo rígido pode ser descrito como uma translação do centro de massa (CM) e uma rotação em torno de um eixo que passa pelo CM, em um total de 6 coordenadas. Definimos as peculiaridades do radiano como unidade de medida do ângulo, que é uma grandeza adimensional. Definimos velocidade e aceleração angulares.

Iniciamos a aula com a revisão do problema 14 da lista 4, em que uma pessoa salta de um veículo parado, que recua. Examinamos com atenção a diferença entre os ângulos de lançamento em relação ao veículo e em relação ao solo.

Introdução da Distribuição de Maxwell-Boltzmann. Cálculo da Energia Média do gás monoatômico
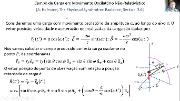
É calculado o campo eletromagnético produzida por uma carga em movimento oscilatório não relativístico

Entender o que é recuo. Usar a transformação de velocidade para montar o sistema de equações. Aplicar conservação da quantidade de movimento quando o recuo importa.

A solução clássica do monopolo magnético de 'Hooft-Polyakov para o grupo de gauge SU(2) e campo de Higgs na representação tripleto (adjunta). Ansatz radial, soluções para as funções perfil, comportamento dos campos no infinito espacial, little grupo U(1) do monopolo.

Fórmula das massas dos bósons de gauge para qualquer representação de um grupo de gauge G. Exemplos de quebra de simetria e grupos de simetria residual.
3685
resultados encontrados